Targeted functionalities
Level 1: core routines specific to a coefficient ring or a polynomial representation
- Code is highly optimized in terms of
work, data locality and parallelism.
- Automatic code generation is used at
library installation time.
- Example: one-dimensional FFT
Level 2: basic arithmetic operations
- Functions provide a variety of algorithmic solutions for a given
operation.
- The user can choose between algorithms
minimizing work or algorithms maximizing parallelism.
- Example: Schönaghe-Strassen, divide-and-conquer,
k-way Toom-Cook and the two-convolution method for
integer polynomial multiplication
Level 3: advanced arithmetic operations
- Functions combine several Level 2 algorithms for achieving a
given task.
- This leads to adaptive algorithms that select appropriate
Level 2 functions depending on available resources (number of cores,
input data size).
- Example: Taylor shift operation
A snapshot of the BPAS ring classes
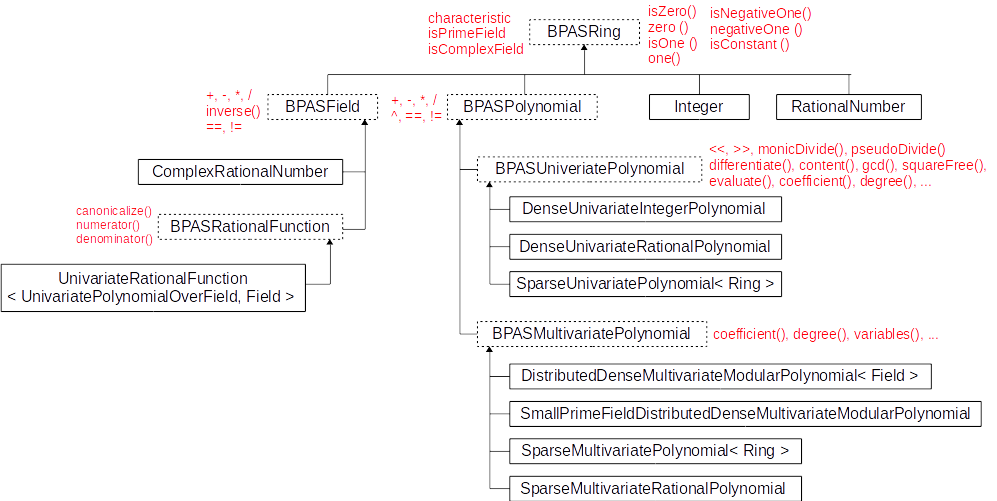
- The BPAS classes Integer and RationalNumber are BPAS wrappers for GMP's
mpz and mpq classes.
- Many other classes are provided, like Intervals, RationalRegularChain, ...
One-dimensional modular FFTs
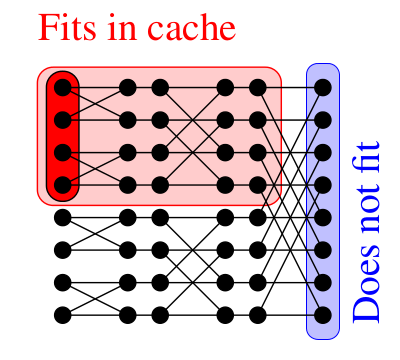
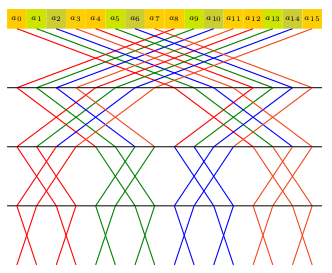
- Assuming an ideal cache of Z words with L words per cache line;
n be the input vector size
- Traditional 2-way FFT proceeds on the FFT graph row-by-row (left picture above)
and a cache complexity in Ω(n / L (log2(n) - log2(Z))), which is not optimal.
- By proceeding in a block-wise manner (picture on the right),
cache complexity becomes
Ο(n / L (log2(n) / log2(Z))),
which is optimal.
- BPAS 1-D FFT code is automatically generated by a
configurable Python script
implementing cache-optimal FFTs.
- In addition to the optimal blocking strategy,
instruction level parallelism (ILP) is
carefully considered: vectorized instructions
are explicitly used (SSE2, SSE4) and instruction
pipeline usage is highly optimized.
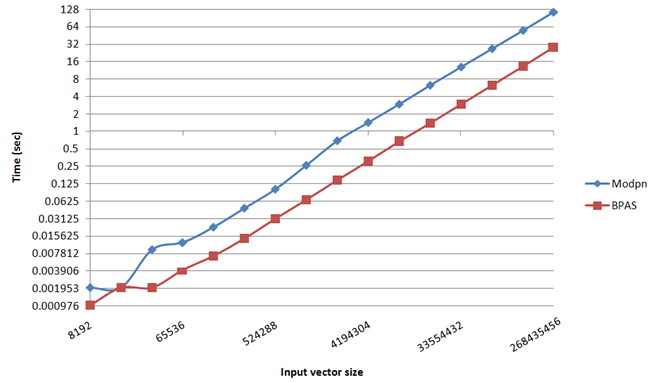
- Experimental results: Modpn (serial) vs BPAS (serial)
Parallel multiplication of dense integer polynomials
- An adaptive algorithm based on the input size and available cores
- Very small: Plain multiplication
- Small or Single-core: Schönaghe-Strassen algorithm via Kronecker's
substitution
- Big but a few cores: Parallel 4-way Toom-Cook
- Big: Parallel 8-way Toom-Cook
- Very big: Parallel two-convolution method
- The two-convolution method
Input: a(y), b(y) ∈ Ζ[y] of degree d with coefficients of bit-size N = K M
Output: the product a(y) b(y)
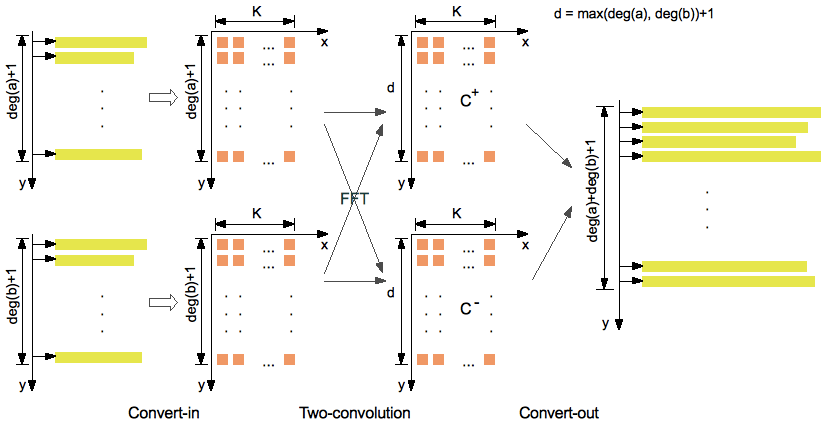
Notations:
- F(e,s) is an upper bound of the number of bot operations
for computing the FFT of a vector of size s
over a prime field Ζ/p with e ∈ Θ(log2(p)).
- If p is a Fourier prime, we have
F(e,s) ∈ Θ(s log2(s) e log2(e) log2log2(e)).
- If e ∈ Θ(log2(s)) and p is a generalized Fermat prime,
then F(e,s) ∈ Θ(s log2(s) e log2log2(e)).
Assumptions (mild):
Algebraic complexity (work, bit ops):
- if p is a Fourier prime, then Ο(d2 log22(d) log2log2log2(d))
(implemented and available)
- if p is a generalized Fermat prime, then
Ο(d2 log2(d) log2log2log2(d))
(work in progress)
- in comparison, Schönaghe-Strassen gives here Ο(d2 log2(d) log2log2(d))
Parallel complexity (span, bit ops):
Ο(log23(d) log2log2log2(d))
Our code relies only and directly on machine
word operations (addition, shift and multiplication).
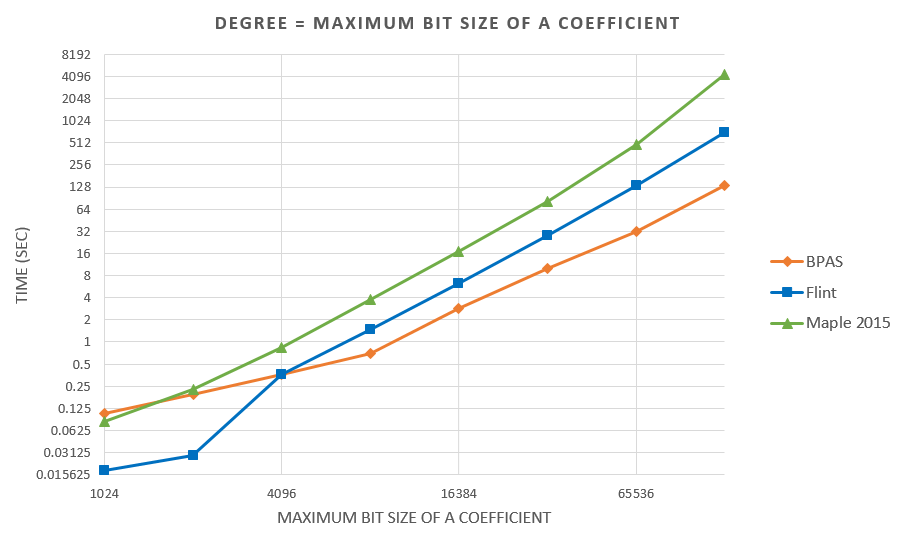
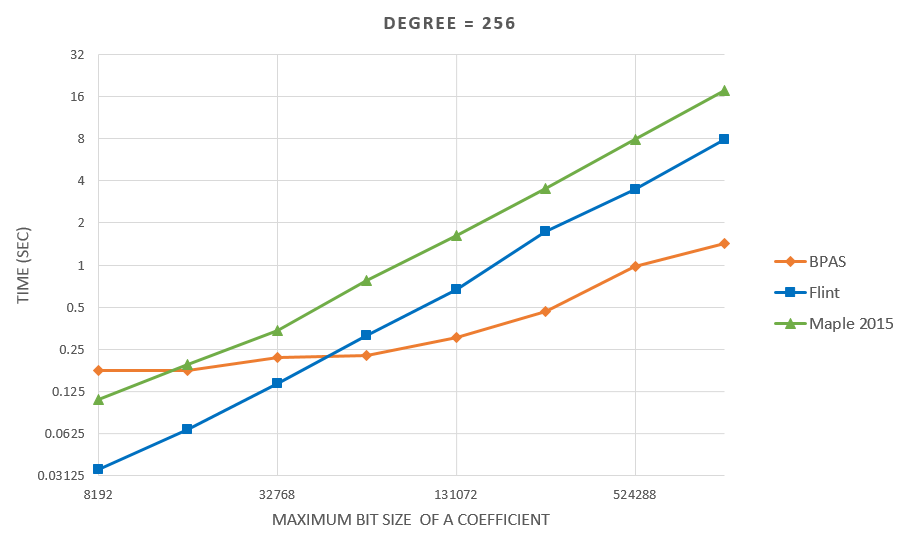
- Experimental results are on a 48-core AMD Opteron 6168 node:
BPAS (parallel) vs FLINT (serial) vs Maple 2015 (parallel)
Symbolic-numeric integration
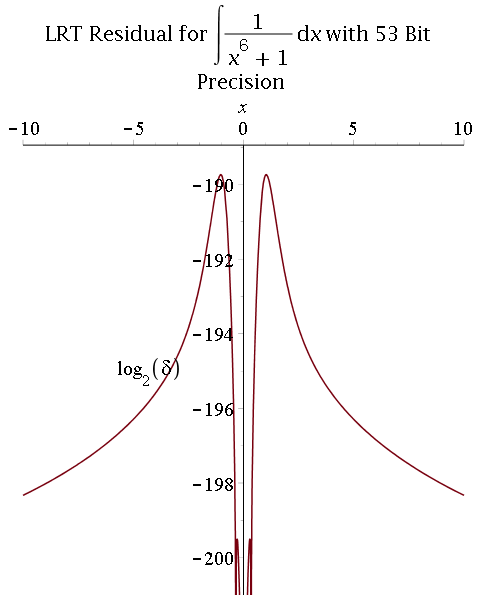
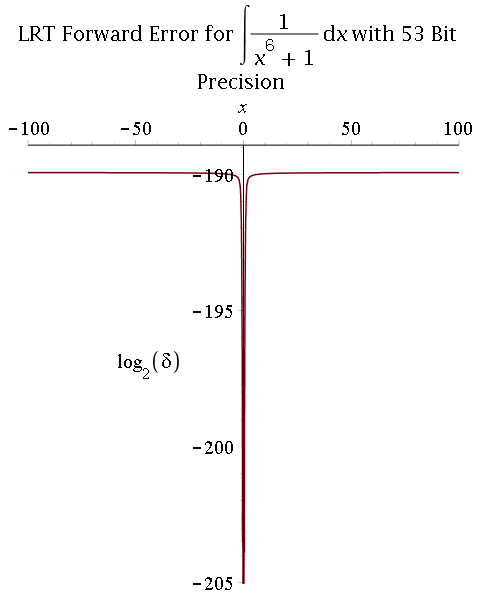
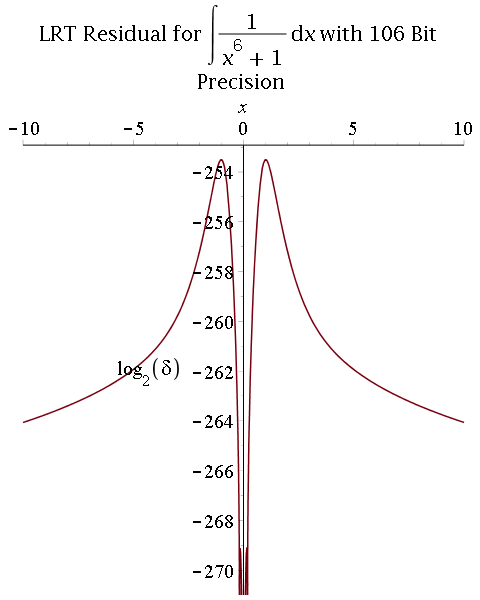
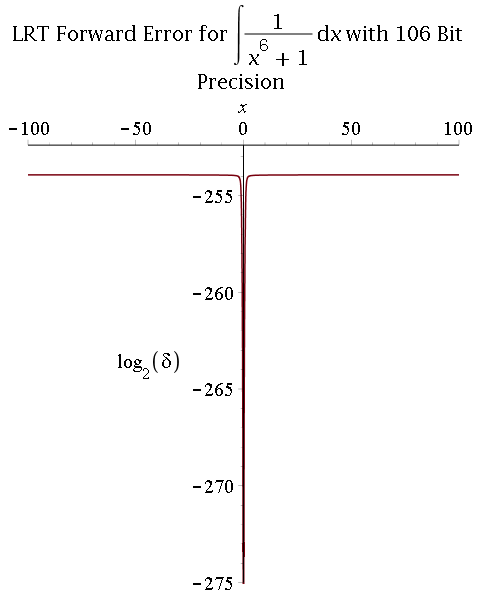
Multiprecision approximate integration of rational functions with error control using two methods:
1) Exact integration followed by a numerical approximation of the integral:
- Hermite reduction (rational part) and Lazard-Rioboo-Trager algorithm (transcendental part) to integrate;
- Multiprecision real-root isolation on factors of the resultant using MPSolve;
- Symbolic post-processing to compute arctangent terms.
- Comparison between 53-bit and 106-bit precisions
2) Multiprecision partial fraction decomposition (PFD) followed by exact integration (proposed by R. Fateman):
- Multiprecision real-root isolation for denominator using MPSolve;
- Symbolic computation of partial fraction decomposition of reconstructed denominator;
- Term-wise integration of rational terms and linear and quadratic (denominator) transcendental terms.
- Comparison between 53-bit and 106-bit precisions:
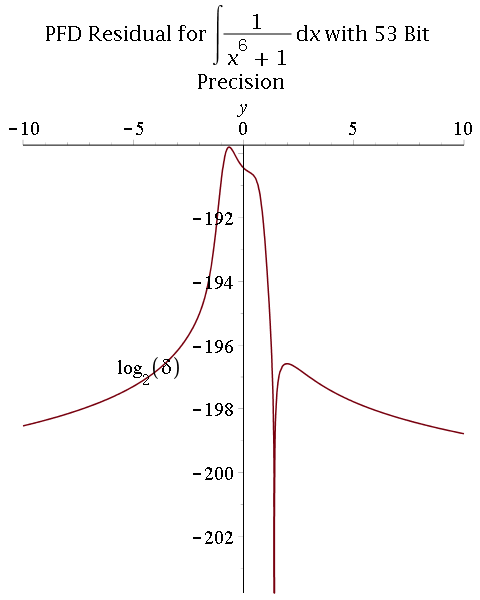
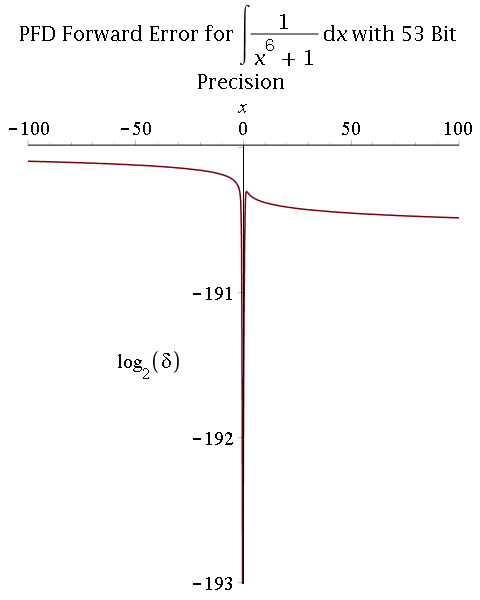
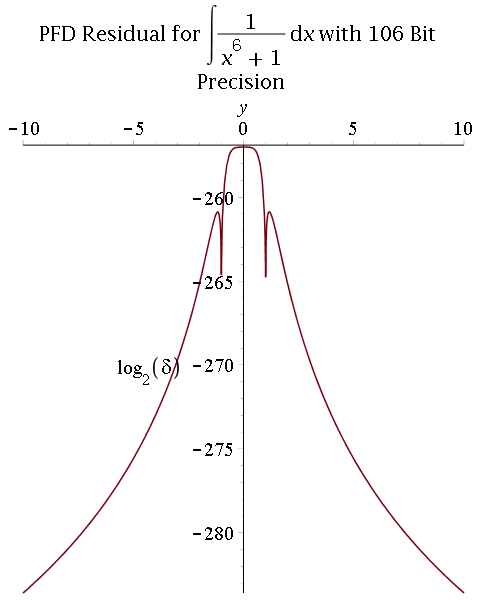
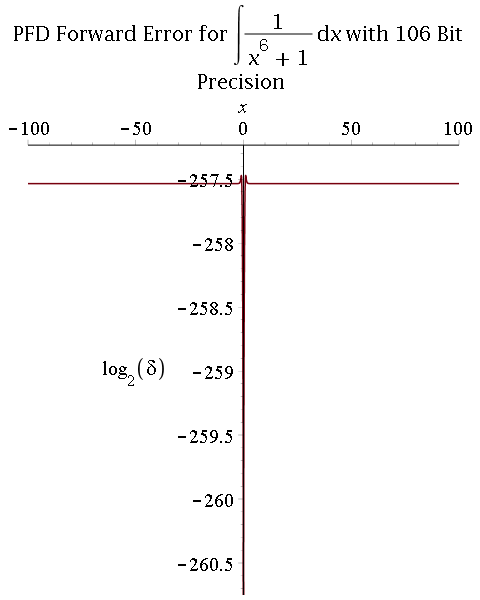

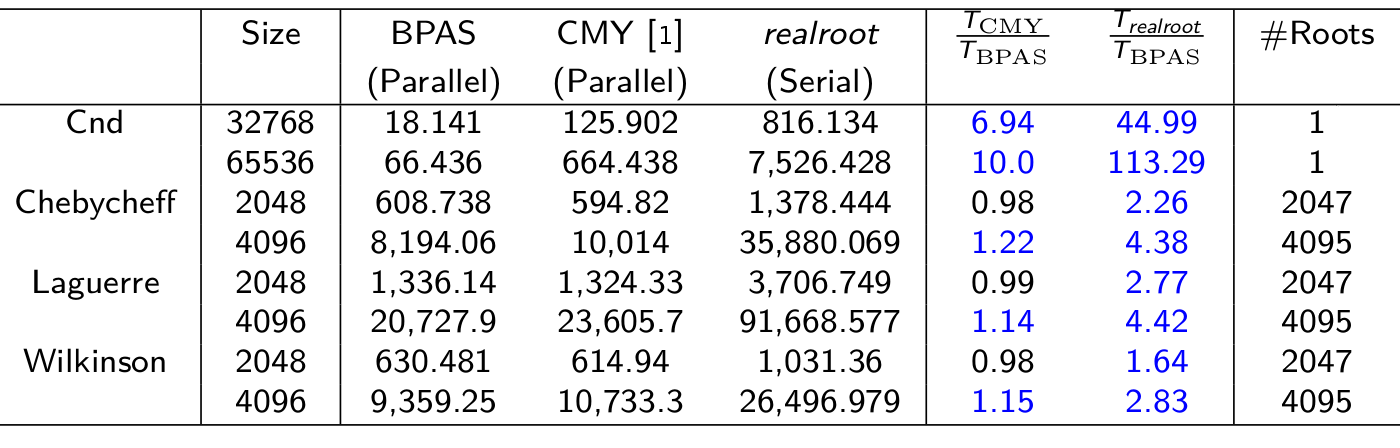
Parallel real root isolation
Parallel univariate real root isolation
- Experimental results: Running time (in sec.) on a 48-core AMD Opteron 6168 node for BPAS (parallel) vs CMY (parallel) vs Maple 18 realroot (serial)
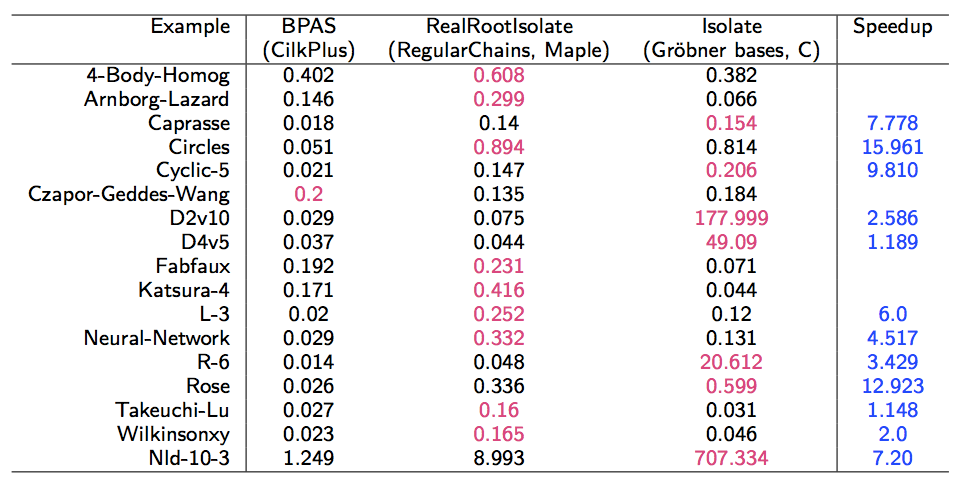
Parallel multivariate real root isolation
- Experimental results: Running time (in sec.) on a 12-core Intel Xeon 5650
node for BPAS (parallel) vs. Maple 17 RealRootIsolate (serial) vs.
C (with Maple 17 interface) Isolate (serial)
ORCCA Lab,
Department of Computer Science,
The University of Western Ontario,
London, Ontario, Canada N6A 5B7